Segment Trees
#algorithmsA segment tree is a data structure that is used to efficiently answers multiple range queries (including updates).
Structure#
Segment tree has a very simple structure; it's a binary tree (represented by an array) that stores information like maximum, minimum, sum, etc., for specific set of range. We can then merge these information to find new information efficiently. For example, for a sum query, we can merge S(A, B) and S(B + 1, C) by adding them to find S(A, C). It's been established that we need only 4x space of the original array to query all possible ranges.
Building a segment tree#
Let the array be: a = [1, 2, 3, 1]
The corresponding segment tree for querying max value will be: tree = [3, 2, 3, 1, 2, 3, 1]
Here's the visual representation of the same:
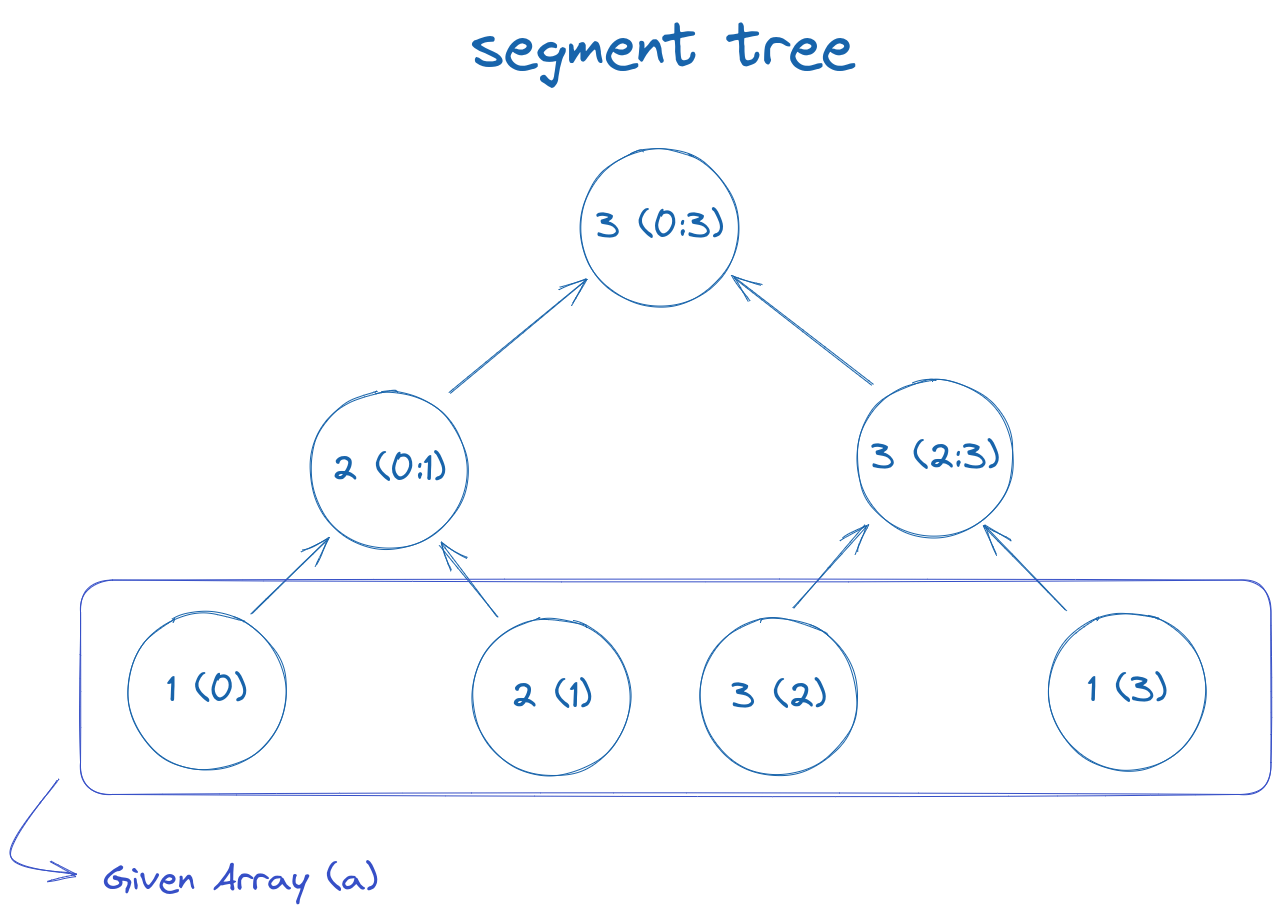
Here tree[0] = a[0:3], tree[1] = a[0:1], tree[2] = a[2:3], tree[3] = a[0:0] and so on.
tree[i] can be easily calculated from it's children by tree[i] = max(tree[2 * i + 1], tree[2 * i + 2]) So, building a segment tree takes O(n) time.
Here's a recursive code for building the tree from array a:
void build(int node, int l, int r) {
if (l == r) {
// leaf node
tree[node] = a[l];
} else {
int mid = (l + r) / 2;
build(2 * node + 1, l, mid); // build left child
build(2 * node + 2, mid + 1, r); // build right child
// set current node after building their children
tree[node] = max(tree[2 * node + 1], tree[2 * node + 2]);
}
}
Quering on segment tree#
After building the tree, we can query for any given range in O(logn) time. We will need to find mutually exclusive and exhaustive nodes that contribute to the given range and merge them.
For example, the mutually exclusive and exhaustive nodes to find the max in range 1-3 are highlighted by red in the following diagram:
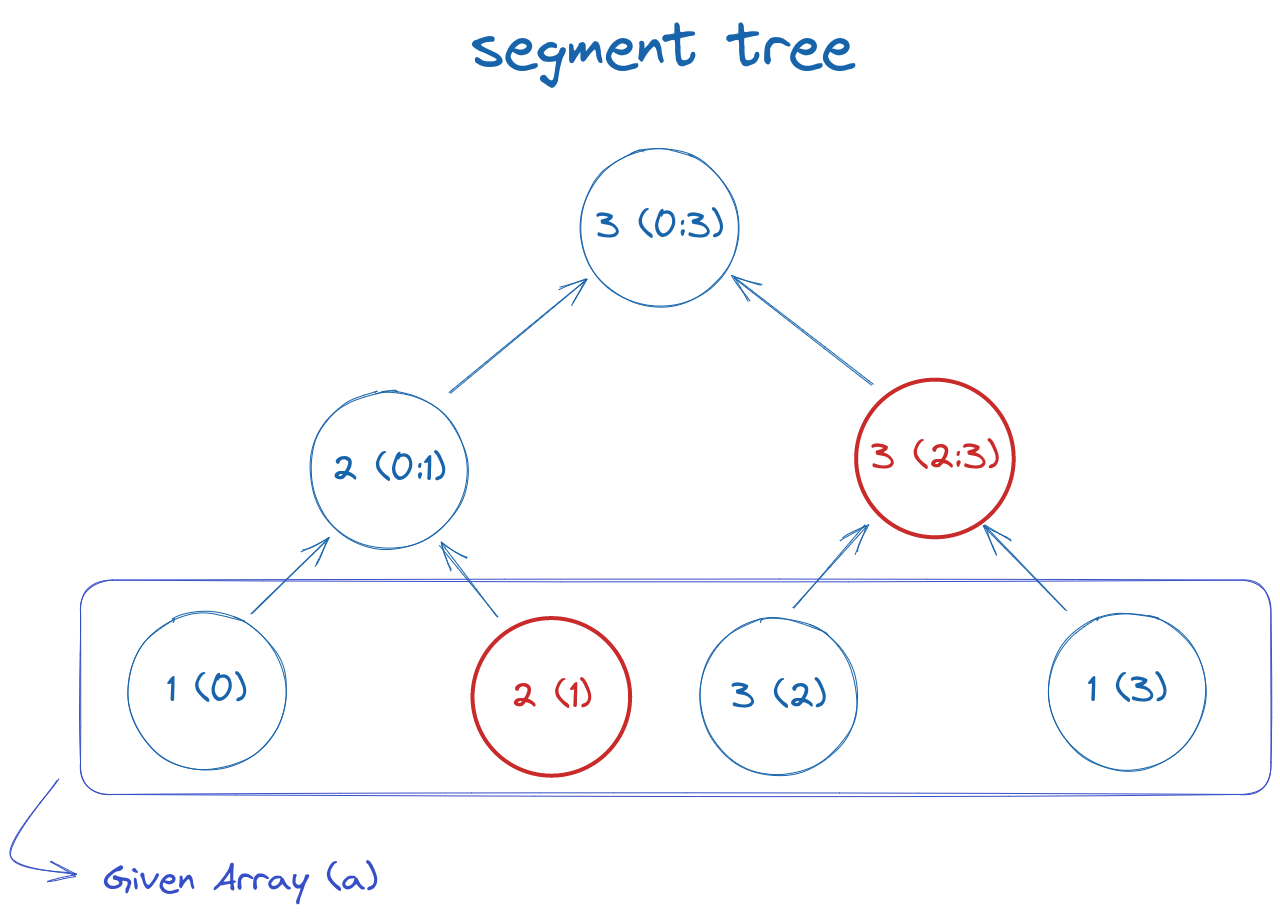
Fortunately, both finding and merging them can be easily done by the following algorithm:
int query(int node, int l, int r, int ql, int qr) {
if (r < l || r < ql) {
// range represented by node is completely outside the given range
return INT_MIN;
}
if (ql <= l && r <= qr) {
// range represented by node is completely inside the given range
return tree[node];
}
// range represented by node is partially inside and partially outside the given range
int mid = (l + r) / 2;
int p1 = query(2 * node + 1, l, mid, ql, qr);
int p2 = query(2 * node + 2, mid + 1, r, ql, qr);
return max(p1, p2);
}
Here (ql, qr) is the given range by a query. We won't go in-depth of tree if the range represented by the current node is completely outside or inside the given range, as seen by the first two if blocks.
To find the sum query, we need to change the last line from return max(p1, p2) to return p1 + p2; and the return statement when completely outside from return INT_MIN; to return 0;.
Updating nodes in the segment tree#
Segment tree is a very flexible data structure and allows efficient updating it's nodes when an array value is modified. The following code is used for updates:
void update(int node, int l, int r, int idx, int val) {
if (l == r) {
// leaf node (here l == r == idx)
a[idx] = val, tree[node] = val;
} else {
int mid = (l + r) / 2;
if (l <= idx && idx <= mid) {
// if idx is in the left child, update left child
update(2 * node + 1, l, mid, idx, val);
} else {
// if idx is in the right child, update right child
update(2 * node + 2, mid + 1, r, idx, val);
}
// update current node after updating either children
tree[node] = max(tree[2 * node + 1], tree[2 * node + 2]);
}
}
We can see that the code is very similar to build. In update, we only update the nodes that will be affected by modifying the array a and go in either left or right child; therefore, the time complexity is O(logn) instead of O(n).
Complete C++ code#
class SegmentTree {
private:
vector<int> tree, a;
public:
SegmentTree(const vector<int>& v) {
int n = v.size();
a = v;
tree.resize(4 * n);
build(0, 0, n - 1);
}
void build(int node, int l, int r) {
if (l == r) {
tree[node] = a[l];
} else {
int mid = (l + r) / 2;
build(node * 2 + 1, l, mid);
build(node * 2 + 2, mid + 1, r);
tree[node] = max(tree[node * 2 + 1], tree[node * 2 + 2]);
}
}
void update(int node, int l, int r, int idx, int val) {
if (l == r) {
a[idx] = val, tree[node] = val;
} else {
int mid = (l + r) / 2;
if (l <= idx && idx <= mid) {
update(2 * node + 1, l, mid, idx, val);
} else {
update(2 * node + 2, mid + 1, r, idx, val);
}
tree[node] = max(tree[2 * node + 1], tree[2 * node + 2]);
}
}
int query(int node, int l, int r, int ql, int qr) {
if (ql > r || qr < l) return INT_MIN; // no overlap
if (ql <= l && qr >= r) return tree[node]; // complete overlap
// partial overlap
int mid = (l + r) / 2;
int left = query(node * 2 + 1, l, mid, ql, qr);
int right = query(node * 2 + 2, mid + 1, r, ql, qr);
return max(left, right);
}
};